Sigmoid curve

What does a sudden outbreak of superheroes, the growth of a new technology, and the spread of a pandemic through the population have in common? The sigmoid curve! If you're a statistician or biologist or any number of -ists, you probably already knew about sigmoid curves. I just learned about it them this week.

A sigmoid curve looks kind of like a squashed S, like this:

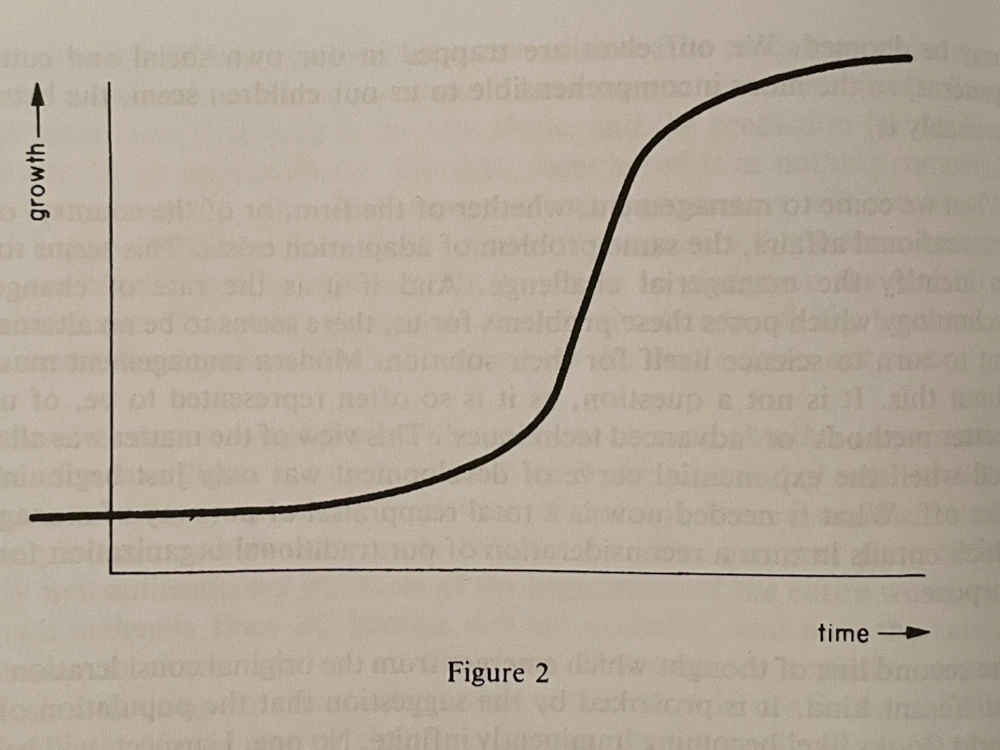
A simple drawing of a sigmoid curve representing growth over time, with neither the units of time or growth specified. Image from Brain of the Firm.

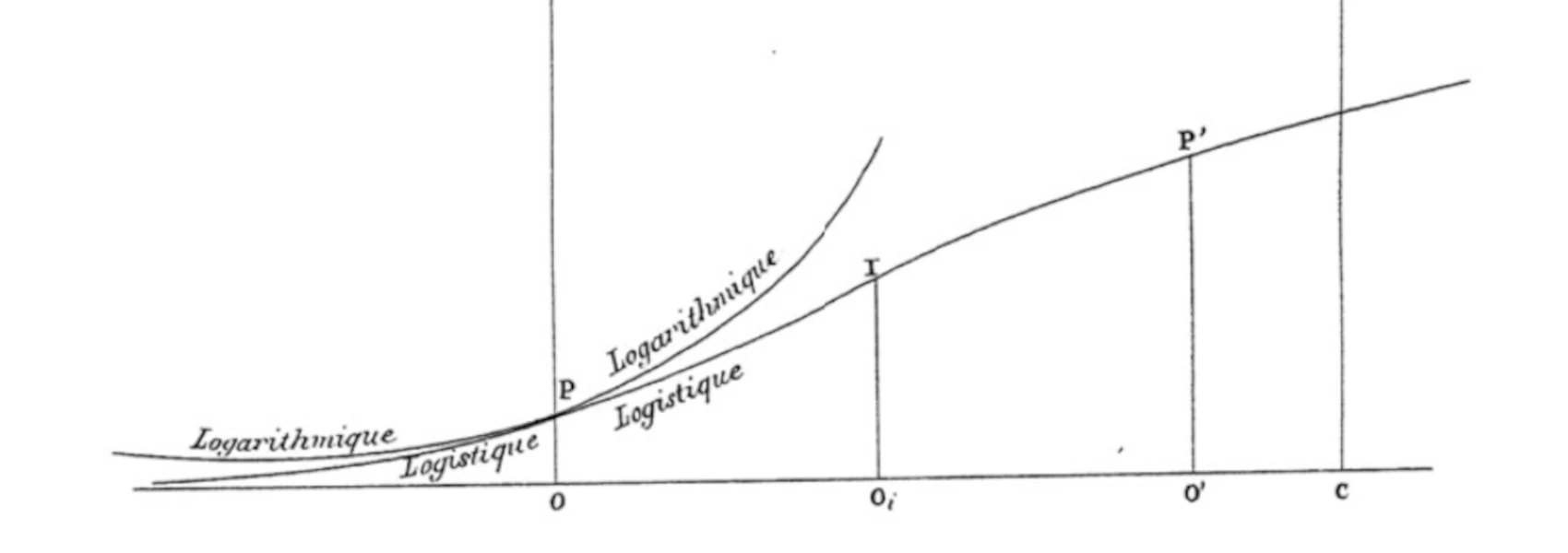
Stafford Beer explains that it is "the typical growth curve which is found in nature."^[1] There are specific types of sigmoid curves, which you can learn all about if you want to go down the merciless mathematical Wikipedia rabbit hole. For example, there are the confusingly-named logistic curve and the Gompertz curve, which is used in pandemic modelling.

One of the interesting things about a sigmoid curve, is that when you're in that middle bit where it's taking off, you can't tell if you're on an exponential or on a sigmoid that will tail off. I was re-reading The Annihilation Score, a Laundry files novel about an outbreak of superhero powers, and the notion came up several times as the characters tried to figure out how big of a problem it would be.

"Oh dear. It's your classic growth curve, starting low and staying low until about three months ago. Then it begins to double. And double again, raising fast, until it hits the dateline. Either the first quartile of a sigmoid curve, or--don't go there--an exponential." The Annihilation Score by Charles Stross, p58

That first mention just sort of blew by me, and it was only later in the book (and sorry, slight spoiler for The Annihilation Score here) that I wondered if it was a wacky idea Stross came up with or another one of those cases were he used a real mathematical or computer science concept and took it in a weird direction:

"As you can see, it seems to be a classic sigmoid curve--suddenly goes from a horizontal line to near-vertical increase, then just as suddenly tails off and goes flat again, albeit at a higher level. We're still working on the confidence limits here, and there's some scope for updating the curve as more low-grade incidents work their way through our reporting system, but it looks, for now, as if we have dodged the bullet. There is no superhero singularity looming in the near future. Just a regular elevated rate at which ordinary people will suddenly acquire enhanced capabilities." The Annihilation Score by Charles Stross, p260

At that point I looked it up and found out that, indeed, a sigmoid curve is a real thing and a type of sigmoid curve, the Gompertz function, is used to model the spread of epidemics. So it was quite appropriate to an outbreak of problematic superhero powers.

I've also been reading Brain of the Firm, one of the foundational books about management cybernetics. In the first chapter, Beer presents several intriguing diagrams about the rate of technological change, to illustrate how alarmingly fast it seems to have been going. He uses the example of human beings top speed of travel:

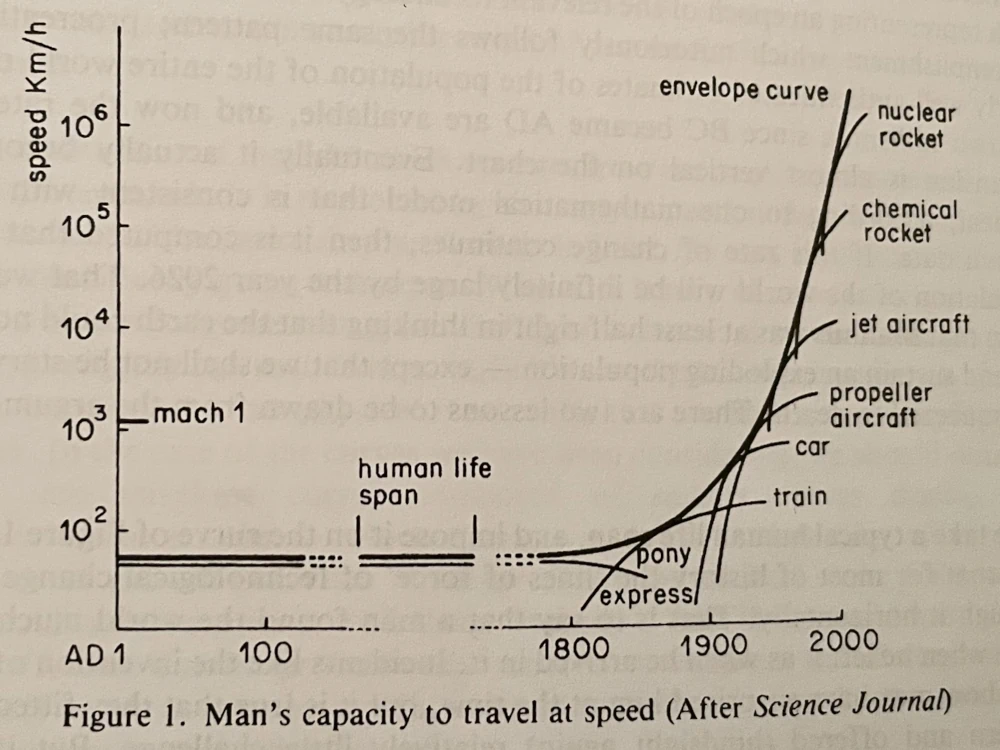
A diagram showing humans capacity to travel at speed dramatically increasing in the last 100 years. Image from Brain of the Firm

Then he explains:

"In the case of the curves we have been considering, we should note that they are envelope curves composed of smaller curves dealing with technological epochs -- which themselves tail off. Now this tailing off is typical of growth processes in nature. Their curves tend to be S-shaped, or sigmoid; mathematicians call them 'logistics'."

Kind of like the fictional analyst in The Annihilation Score, people living through the near-vertical part of the sigmoid curve of a technological epoch might think they are in an exponential. While some exponential scare the crap out of people--like the prospect of exponential population explosion or pandemic deaths--other exponential seem cool and good, like the growth of a technology off of which one is personally making money. So cool and good in fact that it's tempting to give in to the illusion that it will just keep going like this forever.

Beer proposes that you might be able to sustain growth past the tailing off by stringing together novel growth opportunities. Figuring out how to do that seems to be a big point of his book. But, he is quick to add, even this strung together growth of one novel enterprise after another might itself be part of a larger sigmoid curve that will also eventually tail off.

I wonder which technologies are reaching the tailing off point of their natural growth curve after seeming to be on an exponential path forever? I think it will only be possible to really know in retrospect.